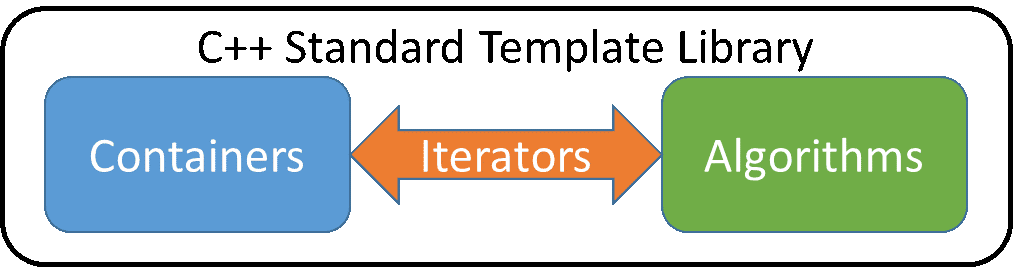
If you’ve programmed in C++ within the last 10 years, you’ve undoubtedly been exposed to the standard template library. The design of the library is really rather profound. This image represents the high level design of the library in a pictorial fashion:
On one hand, the library provides a set of generic container objects that provide a robust implementation of many of the classic data structures available within the field of computer science. The collection of containers includes things like arbitrarily sized contiguous arrays (vectors), linked lists, associative arrays, which are implemented as either binary trees or as a hash container, as well as many more. The set of containers alone make the STL quite valuable for most programmers.
On the other hand, the library provides a set of generic algorithms that encompass a whole suite of functionality defined in classic computer science. Sorting, searching, rearranging, merging, etc… are just a handful of the algorithms provided by the library. Furthermore, extreme care has been taken within the implementation of these algorithms such that an average programmer would hard pressed to produce something safer and more efficient on their own.
However, the real gem of the standard library are iterators. Iterators bridge the gap between generic containers on one side and the generic algorithms on the other side. Need to sort a vector of integers, or a double ended queue of strings? If so, you just call the same sort function and pass it a set of iterators. These iterators “know” how to traverse their parent container. (Remember containers are the data structures.)
So, what if we could write a series of iterators to access data from within an ANSYS result file? What would that buy us? Well, depending upon which concepts our iterators model, having them available would open up access to at least some of the STL suite of algorithms. That’s good. Furthermore, having iterators defined would open up the possibility of providing range objects. If we can provide range objects, then all of the sudden range based for loops are possible. These types of loops are more than just syntactic sugar. By encapsulating the bounds of iteration within a range, and by using iterators in general to perform the iteration, the burden of a correct implementation is placed on the iterators themselves. If you spend the time to get the iterator implementation correct, then any loop you write after that using either the iterators or better yet the range object will implicitly be correct from a loop construct standpoint. Range based for loops also make your code cleaner and easier to reason about locally.
Now for the downside… Iterators are kind of hard to write. The price for the flexibility they offer is paid for in the amount of code it takes to write them. Again, though, the idea is that you (or, better yet somebody else) writes these iterators once and then you have them available to use from that point forward.
Because of their flexibility, standard conformant iterators come in a number of different flavors. In fact, they are very much like an ice cream Sunday where you can pick and choose what features to mix in or add on top. This is great, but again it makes implementing them a bit of a chore. Here are some of the design decisions you have to answer when implementing an iterator:
| Decision | Options | Choice for RST Reader Iterators |
| Dereference Data Type | Anything you want | Special structs for each type of iterator. |
| Iteration Category | 1. Forward iterator 2. Single pass iterator 3. Bidirectional iterator 4. Random access iterator |
Forward, Single Pass |
Iterators syntactically function much like pointers in C or C++. That is, like a pointer you can increment an iterator with the ++ operator, you can dereference an iterator with the * operator and you can compare two iterators for equality. We will talk more about incrementing and comparisons in a minute, but first let’s focus on dereferencing. One thing we have to decide is what type of data the client of our iterator will receive when they dereference it. My choice is to return a simple C++ structure with data members for each piece of data. For example, when we are iterating over the nodal geometry, the RST file contains the node number, the nodal coordinates and the nodal rotations. To represent this data, I create a structure like this: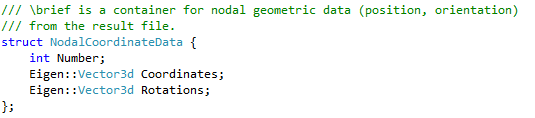
I think this is pretty self-explanatory. Likewise, if we are iterating over the element geometry section of an RST file, there is quite a bit of useful information for each element. The structure I use in that case looks like this:
Again, pretty self-explanatory. So, when I’m building a node geometry iterator, I’m going to choose the NodalCoordinateData structure as my dereference type.
The next decision I have to make is what “kind” of iterator I’m going to create. That is, what types of “iteration” will it support? The C++ standard supports a variety of iterator categories. You may be wondering why anyone would ever care about an “iteration category”? Well, the reason is fundamental to the design of the STL. Remember that the primary reason iterators exist is to provide a bridge between generic containers and generic algorithms. However, any one particular algorithm may impose certain requirements on the underlying iterator for the algorithm to function appropriately.
Take the algorithm “sort” for example. There are, in fact, lots of different “sort” algorithms. The most efficient versions of the “sort” algorithm require that an iterator be able to jump around randomly in constant time within the container. If the iterator supports jumping around (a.k.a. random access) then you can use it within the most efficient sort algorithm. However, there are certain kinds of iterators that don’t support jumping around. Take a linked list container as an example. You cannot randomly jump around in a linked list in constant time. To get to item B from item A you have to follow the links, which means you have to jump from link to link to link, where each jump takes some amount of processing time. This means, for example, there is no easy way to cut a linked list exactly in half even if you know how many items in total are in the list. To cut it in half you have to start at the beginning and follow the links until you’ve followed size/2 number of links. At that point you are at the “center” of the list. However, with an array, you simply choose an index equal to size/2 and you automatically get to the center of the array in one step. Many sort algorithms, as an example, obtain their efficiency by effectively chopping the container into two equal pieces and recursively sorting the two pieces. You lose all that efficiency if you have to walk out to the center.
If you look at the “types” of iterators in the table above you will see that they build upon one another. That is, at the lowest level, I have to answer the question, can I just move forward one step? If I can’t even do that, then I’m not an iterator at all. After that, assuming I can move forward one step, can I only go through the range once, or can I go over the range multiple times? If I can only go over the range once, I’m a single pass iterator. Truthfully, the forward iterator concept and the single pass iterator concept form level 1A and 1B of the iterator hierarchy. The next higher level of functionality is a bidirectional iterator. This type of iterator can go forward and backwards one step in constant time. Think of a doubly linked list. With forward and backward links, I can go either direction one step in constant time. Finally, the most flexible iterator is the random access iterator. These are iterators that really are like raw pointers. With a pointer you can perform pointer arithmetic such that you can add an arbitrary offset to a base pointer and end up at some random location in a range. It’s up to you to make sure that you stay within bounds. Certain classes of iterators provide this level of functionality, namely those associated with vectors and deques.
So, the question is what type of iterator should we support? Perusing through the FORTRAN code shipped with ANSYS, there doesn’t appear to be an inherent limitation within the functions themselves that would preclude random access. But, my assumption is that the routines were designed to access the data sequentially. (At least, if I were the author of the functions that is what I would expect clients to do.) So, I don’t know how well they would be tested regarding jumping around. Furthermore, disk controllers and disk subsystems are most likely going to buffer the data as it is read, and they very likely perform best if the data access is sequential. So, even if it is possible to randomly jump around on the result file, I’m not sold on it being a good idea from a performance standpoint. Lastly, I explicitly want to keep all of the data on the disk, and not buffer large chunks of it into RAM within my library. So, I settled on expressing my iterators as single pass, forward iterators. These are fairly restrictive in nature, but I think they will serve the purpose of reading data off of the file quite nicely.
Regarding my choice to not buffer the data, let me pause for a minute and explain why I want to keep the data on the disk. First, in order to buffer the data from disk into RAM you have to read the data off of the disk one time to fill the buffer. So, that process automatically incurs one disk read. Therefore, if you only ever need to iterate over the data once, perhaps to load it into a more specialized data structure, buffering it first into an intermediate RAM storage will actually slow you down, and consume more RAM. The reason for this is that you would first iterate over the data stored on the disk and read it into an intermediate buffer. Then, you would let your client know the data is ready and they would iterate over your internal buffer to access the data. They might as well just read the data off the disk themselves! If the end user really wants to buffer the data, that’s totally fine. They can choose to do that themselves, but they shouldn’t have to pay for it if they don’t need it.
Finally, we are ready to implement the iterators themselves. To do this I rely on a very high quality open source library called Boost. Boost has within it a library called iterator_facade that takes care of supplying most all of the boilerplate code needed to create a conformant iterator. Using it has proven to be a real time saver. To define the actual iterator, you derive your iterator class from iterator_facade and pass it a few template parameters. One is the category defining the type of iterator you are creating. Here is the definition for the nodal geometry iterator:
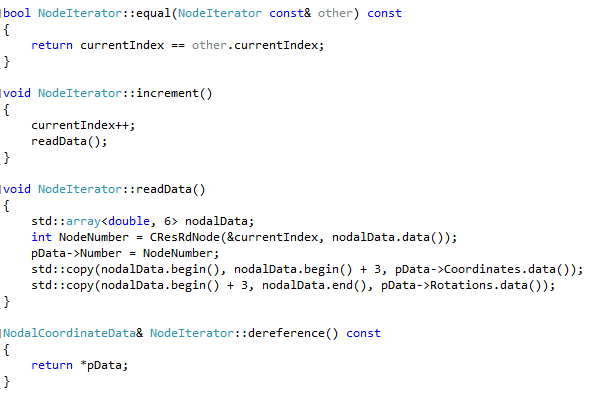
You can see that there are a few private functions here that actually do all of the work. The function “increment” is responsible for moving the iterator forward one spot. The function “equal” is responsible for determining if two different iterators are in fact equal. And the function “dereference” is used to return the data associated with the current iteration spot. You will also notice that I locally buffer the single piece of data associated with the current location in the iteration space inside the iterator. This is stored in the pData member function. I also locally store the current index. Here are the implementations of the functions just mentioned:
First you can see that testing iterator equality is easy. All we do is just look to see if the two iterators are pointing to the same index. If they are, we define them as equal. (Note, an important nuance of this is that we don’t test to see if their buffered data is equal, just their index. This is important later on.) Likewise, increment is easy to understand as well. We just increase the index by one, and then buffer the new data off of disk into our local storage. Finally, dereference is easy too. All we do here is just return a reference to the local data store that holds this one node’s data. The only real work occurs in the readData() function. Inside that function you will see the actual call to the CResRdNode() function. We pass that function our current index and it populates an array of 6 doubles with data and returns the actual node number. After we have that, we simply parse out of that array of 6 doubles the coordinates and rotations, storing them in our local storage. That’s all there is to it. A little more work, but not bad.
With these handful of operations, the boost iterator_facade class can actually build up a fully conformant iterator will all the proper operator overloads, etc… It just works. Now that we have iterators, we need to provide a “begin” and “end” function just like the standard containers do. These functions should return iterators that point to the beginning of our data set and to one past the end of our data set. You may be thinking to yourself, wait a minute, how to we provide an “end” iterator without reading the whole set of nodes? The reality is, we just need to provide an iterator that “equality tests” to be equal to the end of our iteration space? What does that mean? Well, what it means is that we just need to provide an iterator that, when compared to another iterator which has walked all the way to the end, it passes the “equal” test. Look at the “equal” function above. What do two iterators need to have in common to be considered equal? They need to have the same index. So, the “end” iterator simply has an index equal to one past the end of the iteration space. We know how big our iteration space is because that is one of the pieces of metadata supplied by those ResRd*Begin functions. So, here are our begin/end functions to give us a pair of conformant iterators.
Notice, that the nodes_end() function creates a NodeIterator and passes it an index that is one past the maximum number of nodes that have coordinate data stored on file. You will also notice, that it does not have a second Boolean argument associated with it. I use that second argument to determine if I should immediately read data off of the disk when the iterator is constructed. For the begin iterator, I need to do that. For the end iterator, I don’t actually need to cache any data. In fact, no data for that node is defined on disk. I just need a sentinel iterator that is one past the iteration space.
So, there you have it. Iterators are defined that implicitly walk over the rst file pulling data off as needed and locally buffering one piece of it. These iterators are standard conformant and thus can be used with any STL algorithm that accepts a single pass, read only, forward iterator. They are efficient in time and storage. There is, though, one last thing that would be nice. That is to provide a range object so that we can have our cake and eat it too. That is, so we can write these C++11 range based for loops. Like this: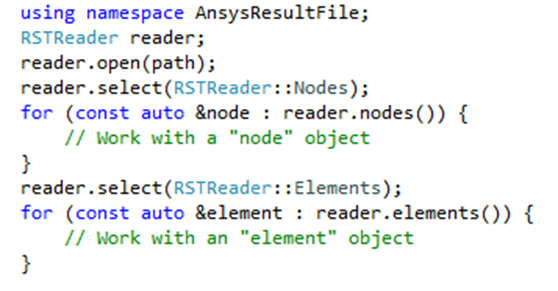
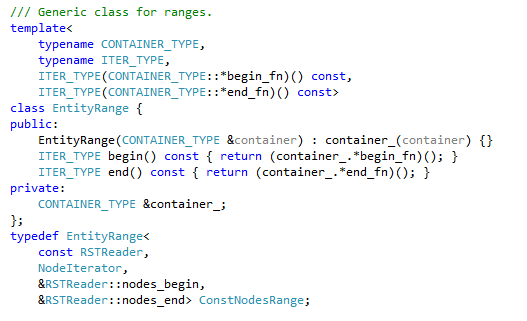
To do that we need a bit of template magic. Consider this template and type definition:
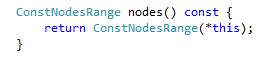
There is a bit of machinery that is going on here, but the concept is simple. I just want the compiler to stamp out a new type that has a “begin()” and “end()” member function that actually call my “nodes_begin()” and “nodes_end()” functions. That is what this template will do. I can also create a type that will call my “elements_begin()” and “elements_end()” function. Once I have those types, creating range objects suitable for C++11 range based for loops is a snap. You just make a function like this:
This function creates one of these special range types and passes in a pointer to our RST reader. When the compiler then sees this code:
It sees a range object as the return type of the “nodes()” function. That range object is compatible with the semantics of range based for loops, and therefore the compiler happily generates code for this construction.
Now, after all of this work, the client of the RST reader library can open a result file, select something of interest, and start looping over the items in that category; all in three lines of code. There is no need to understand the nuances of the binlib functions. But best of all, there is no appreciable performance hit for this abstraction. At the end of the day, we’re not computationally doing anything more than what a raw use of the binlib functions would perform. But, we’re adding a great deal of type safety, and, in my opinion, readability to the code. But, then again, I’m only slightly partial to C++. Your mileage may vary…