How can the mechanical behavior of cellular structures (honeycombs, foams and lattices) be modeled?
This is the second in a two-part post on the modeling aspects of 3D printed cellular structures. If you haven’t already, please read the first part here, where I detail the challenges associated with modeling 3D printed cellular structures.
The literature on the 3D printing of cellular structures is vast, and growing. While the majority of the focus in this field is on the design and process aspects, there is a significant body of work on characterizing behavior for the purposes of developing analytical material models. I have found that these approaches fall into 3 different categories depending on the level of discretization at which the property is modeled: at the level of each material point, or at the level of the connecting member or finally, at the level of the cell. At the end of this article I have compiled some of the best references I could find for each of the 3 broad approaches.
1. Continuum Modeling
The most straightforward approach is to use bulk material properties to represent what is happening to the material at the cellular level [1-4]. This approach does away with the need for any cellular level characterization and in so doing, we do not have to worry about size or contact effects described in the previous post that are artifacts of having to characterize behavior at the cellular level. However, the assumption that the connecting struts/walls in a cellular structure behave the same way the bulk material does can particularly be erroneous for AM processes that can introduce significant size specific behavior and large anisotropy. It is important to keep in mind that factors that may not be significant at a bulk level (such as surface roughness, local microstructure or dimensional tolerances) can be very significant when the connecting member is under 1 mm thick, as is often the case.
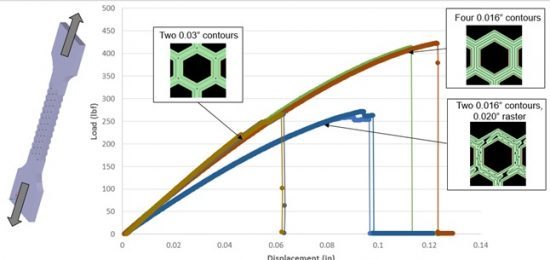
The level of error introduced by a continuum assumption is likely to vary by process: processes like Fused Deposition Modeling (FDM) are already strongly anisotropic with highly geometry-specific meso-structures and an assumption like this will generate large errors as shown in Figure 1. On the other hand, it is possible that better results may be had for powder based fusion processes used for metal alloys, especially when the connecting members are large enough and the key property being solved for is mechanical stiffness (as opposed to fracture toughness or fatigue life).
2. Cell Level Homogenization
The most common approach in the literature is the use of homogenization – representing the effective property of the cellular structure without regard to the cellular geometry itself. This approach has significantly lower computational expense associated with its implementation. Additionally, it is relatively straightforward to develop a model by fitting a power law to experimental data [5-8] as shown in the equation below, relating the effective modulus E* to the bulk material property Es and their respective densities (ρ and ρs), by solving for the constants C and n.
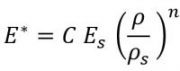
While a homogenization approach is useful in generating comparative, qualitative data, it has some difficulties in being used as a reliable material model in analysis & simulation. This is first and foremost since the majority of the experiments do not consider size and contact effects. Secondly, even if these were considered, the homogenization of the cells only works for the specific cell in question (e.g. octet truss or hexagonal honeycomb) – so every new cell type needs to be re-characterized. Finally, the homogenization of these cells can lose insight into how structures behave in the transition region between different volume fractions, even if each cell type is calibrated at a range of volume fractions – this is likely to be exacerbated for failure modeling.
3. Member Modeling
The third approach involves describing behavior not at each material point or at the level of the cell, but at a level in-between: the connecting member (also referred to as strut or beam). This approach has been used by researchers [9-11] including us at PADT [12] by invoking beam theory to first describe what is happening at the level of the member and then use that information to build up to the level of the cells.
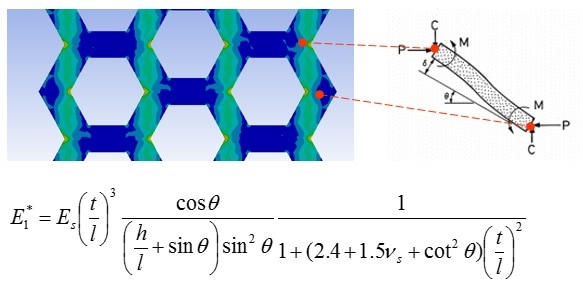
This approach, while promising, is beset with some challenges as well: it requires experimental characterization at the cellular level, which brings in the previously mentioned challenges. Additionally, from a computational standpoint, the validation of these models typically requires a modeling of the full cellular geometry, which can be prohibitively expensive. Finally, the theory involved in representing member level detail is more complex, makes assumptions of its own (e.g. modeling the “fixed” ends) and it is not proven adequately at this point if this is justified by a significant improvement in the model’s predictability compared to the above two approaches. This approach does have one significant promise: if we are able to accurately describe behavior at the level of a member, it is a first step towards a truly shape and size independent model that can bridge with ease between say, an octet truss and an auxetic structure, or different sizes of cells, as well as the transitions between them – thus enabling true freedom to the designer and analyst. It is for this reason that we are focusing on this approach.
Conclusion
Continuum models are easy to implement and for relatively isotropic processes and materials such as metal fusion, may be a good approximation of stiffness and deformation behavior. We know through our own experience that these models perform very poorly when the process is anisotropic (such as FDM), even when the bulk constitutive model incorporates the anisotropy.
Homogenization at the level of the cell is an intuitive improvement and the experimental insights gained are invaluable – comparison between cell type performances, or dependencies on member thickness & cell size etc. are worthy data points. However, caution needs to be exercised when developing models from them for use in analysis (simulation), though the relative ease of their computational implementation is a very powerful argument for pursuing this line of work.
Finally, the member level approach, while beset with challenges of its own, is a promising direction forward since it attempts to address behavior at a level that incorporates process and geometric detail. The approach we have taken at PADT is in line with this approach, but specifically seeks to bridge the continuum and cell level models by using cellular structure response to extract a point-wise material property. Our preliminary work has shown promise for cells of similar sizes and ongoing work, funded by America Makes, is looking to expand this into a larger, non-empirical model that can span cell types. If this is an area of interest to you, please connect with me on LinkedIn for updates. If you have questions or comments, please email us at info@padtinc.com or drop me a message on LinkedIn.
References (by Approach)
Bulk Property Models
[1] C. Neff, N. Hopkinson, N.B. Crane, “Selective Laser Sintering of Diamond Lattice Structures: Experimental Results and FEA Model Comparison,” 2015 Solid Freeform Fabrication Symposium
[2] M. Jamshidinia, L. Wang, W. Tong, and R. Kovacevic. “The bio-compatible dental implant designed by using non-stochastic porosity produced by Electron Beam Melting®(EBM),” Journal of Materials Processing Technology214, no. 8 (2014): 1728-1739
[3] S. Park, D.W. Rosen, C.E. Duty, “Comparing Mechanical and Geometrical Properties of Lattice Structure Fabricated using Electron Beam Melting”, 2014 Solid Freeform Fabrication Symposium
[4] D.M. Correa, T. Klatt, S. Cortes, M. Haberman, D. Kovar, C. Seepersad, “Negative stiffness honeycombs for recoverable shock isolation,” Rapid Prototyping Journal, 2015, 21(2), pp.193-200.
Cell Homogenization Models
[5] C. Yan, L. Hao, A. Hussein, P. Young, and D. Raymont. “Advanced lightweight 316L stainless steel cellular lattice structures fabricated via selective laser melting,” Materials & Design 55 (2014): 533-541.
[6] S. Didam, B. Eidel, A. Ohrndorf, H.‐J. Christ. “Mechanical Analysis of Metallic SLM‐Lattices on Small Scales: Finite Element Simulations versus Experiments,” PAMM 15.1 (2015): 189-190.
[7] P. Zhang, J. Toman, Y. Yu, E. Biyikli, M. Kirca, M. Chmielus, and A.C. To. “Efficient design-optimization of variable-density hexagonal cellular structure by additive manufacturing: theory and validation,” Journal of Manufacturing Science and Engineering 137, no. 2 (2015): 021004.
[8] M. Mazur, M. Leary, S. Sun, M. Vcelka, D. Shidid, M. Brandt. “Deformation and failure behaviour of Ti-6Al-4V lattice structures manufactured by selective laser melting (SLM),” The International Journal of Advanced Manufacturing Technology 84.5 (2016): 1391-1411.
Beam Theory Models
[9] R. Gümrük, R.A.W. Mines, “Compressive behaviour of stainless steel micro-lattice structures,” International Journal of Mechanical Sciences 68 (2013): 125-139
[10] S. Ahmadi, G. Campoli, S. Amin Yavari, B. Sajadi, R. Wauthle, J. Schrooten, H. Weinans, A. Zadpoor, A. (2014), “Mechanical behavior of regular open-cell porous biomaterials made of diamond lattice unit cells,” Journal of the Mechanical Behavior of Biomedical Materials, 34, 106-115.
[11] S. Zhang, S. Dilip, L. Yang, H. Miyanji, B. Stucker, “Property Evaluation of Metal Cellular Strut Structures via Powder Bed Fusion AM,” 2015 Solid Freeform Fabrication Symposium
[12] D. Bhate, J. Van Soest, J. Reeher, D. Patel, D. Gibson, J. Gerbasi, and M. Finfrock, “A Validated Methodology for Predicting the Mechanical Behavior of ULTEM-9085 Honeycomb Structures Manufactured by Fused Deposition Modeling,” Proceedings of the 26th Annual International Solid Freeform Fabrication, 2016, pp. 2095-2106