ANSYS Mechanical – Overcoming Convergence Difficulties with the Semi-Implicit Method

In our last blog, we discussed using Nonlinear Adaptive Region to overcome convergence difficulties by having the solver automatically trigger a remesh when elements have become excessively distorted.  You can read it here:  https://www.padtinc.com/blog/ansys-mechanical-overcoming-convergence-difficulties-with-automatic-remeshing-nonlinear-adaptive-region/

This time we look at another tool for overcoming convergence difficulties, the Semi-Implicit method.  ANSYS, Inc. describes the semi-implicit method as a hybrid, combining features of both implicit and explicit finite element methods.

In highly nonlinear problems involving significant deformations we may get a solver error like this one: 

*** ERROR ***                           CP =   18110.688   TIME= 11:58:42
Solution not converged at time 0.921 (load step 1 substep 185).           Run terminated. 

Like it does with other problems that lead to convergence failures, the Solution branch will have telltale red lightning bolts, indicating the solution was not able to complete due to nonconvergence.

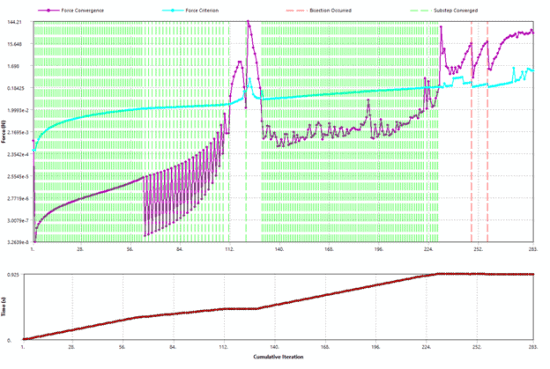
In this case, it can be difficult to determine from the error message in the solution output exactly what the problem is.  Plotting the Newton-Raphson residuals can be a good starting point.  In order to plot the Newton-Raphson residuals, though, we need to turn them on prior to solving.  See this older Focus blog for instructions on how to do that:

https://www.padtinc.com/blog/overcoming-convergence-difficulties-in-ansys-workbench-mechanical-part-i-using-newton-raphson-residual-information/

A plot of the Newton-Raphson residuals shows us where the highest force imbalance is in the model:

That’s a nice looking plot, but doesn’t tell us much without knowing more about the simulation.  The model is of a plastic bottle, subject to a force load tending to ‘crush’ the bottle from top to bottom.  There is a slight off center load as well, so that the force is not purely in the downward direction. 

The bottle is constrained with a fixed support on the bottom flat surface, and contact elements between the outer surface of the bottle and a fixed surface representing a table or floor.  This is to prevent the bottle from deflecting below the plane of that surface.

The material used is a polyethylene plastic, from the ANSYS Granta Materials Data for Simulation add-on, which is a great tool to get access to hundreds of materials for ANSYS simulations.  The geometry of the bottle was created in SpaceClaim as a surface body and meshed with shell elements in ANSYS Mechanical. 

The solution was run as nonlinear static, with large deflection effects turned on.  Automatic Time Stepping was manually activated with a starting and minimum number of substeps set to 200 and a maximum number of substeps set to 1000.

With these settings, the solution ran to about 92% of the full load, where it failed to solve after bisecting to the maximum number of substeps (minimum ‘time’ step).  The force convergence plots showed the bisections and failed convergence attempts started at about iteration 230 and ‘time’ 0.92.  (If you are not familiar with the convergence plots from a Newton-Raphson method solution, please see our Focus archives for an article on the topic – look for the link to the GST Plot:  https://www.padtinc.com/blog2/wp-content/uploads/oldblog/PADT_TheFocus_08.pdf).

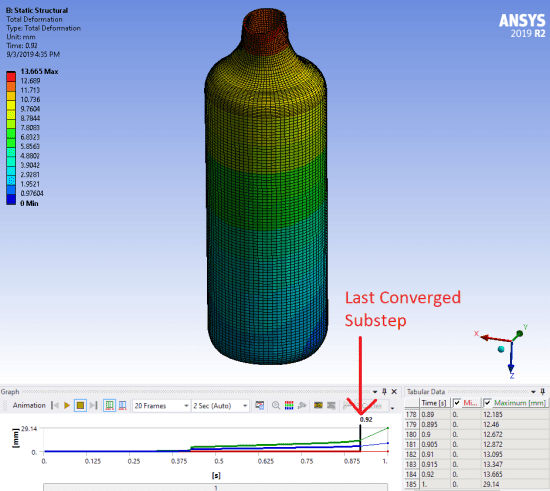
Even though our solution has not converged, it is probably helpful to view the deformation results for substeps which did converge (at partial load) as well as the unconverged results which will be written as the last set of results.

This plot shows the total deformation at the last converged substep (time value 0.92):

This plot shows the unconverged solution, ‘extrapolated’ to time 1.0:

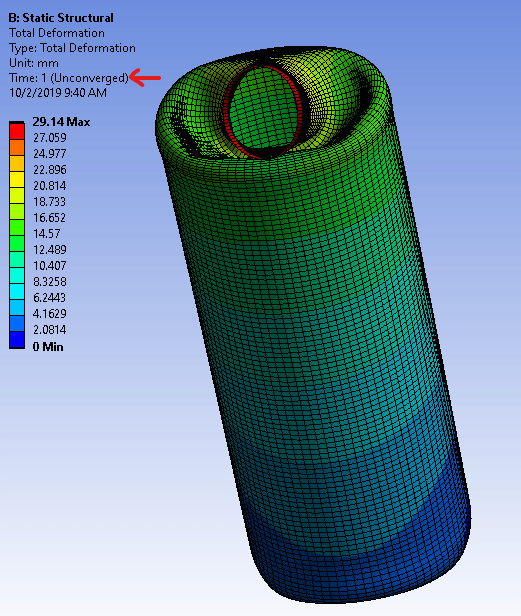
From the unconverged deformation plot we can see that the top of the bottle is tending to experience very large deformations.  It’s not surprizing that convergence difficulties are being encountered.

One of the techniques we can utilize to get past this problem is the Semi-Implicit method in ANSYS Mechanical.  As of 2019 R2, this needs to be activated using a Mechanical APDL command object, but it can be as simple as adding a single word within the Static Structural branch:

SEMIIMPLICIT

There are some optional fields on that command, but minimally just the one word command is needed.

Once the semi-implicit method is activated, if the solver detects the default implicit solver is having trouble, it automatically switches to the semi-implicit solving scheme.  Like a traditional explicit solver, the semi-implicit method can better handle very large deformation, transitory-like effects.  The method can switch back to implicit if conditions warrant for a more efficient solution and in fact can switch back and forth between the two schemes.

The solver output will tell us if the semi-implicit scheme has been activated:

EQUIL ITER  26 COMPLETED.  NEW TRIANG MATRIX.  MAX DOF INC=  0.9526   

     NONLINEAR DIAGNOSTIC DATA HAS BEEN WRITTEN TO  FILE: file.nd004

     DISP CONVERGENCE VALUE   =  0.3918      CRITERION=   1.448     <<< CONVERGED

     LINE SEARCH PARAMETER =  0.4113     SCALED MAX DOF INC =  0.3918   

     FORCE CONVERGENCE VALUE  =   44.44      CRITERION=  0.9960   

     MOMENT CONVERGENCE VALUE =   3.263      CRITERION=  0.1423   

    Writing NEWTON-RAPHSON residual forces to file: file.nr001

    >>> TRANSITIONING TO SEMI-IMPLICIT METHOD

     NONLINEAR DIAGNOSTIC DATA HAS BEEN WRITTEN TO  FILE: file.nd001


    EQUIL ITER   1 COMPLETED.  NEW TRIANG MATRIX.  MAX DOF INC=  0.8788E-04

     NONLINEAR DIAGNOSTIC DATA HAS BEEN WRITTEN TO  FILE: file.nd002

 *** LOAD STEP     1   SUBSTEP   185  COMPLETED.    CUM ITER =    284

 *** TIME =  0.920010         TIME INC =  0.100000E-04

    Kinetic Energy = 0.2157        Potential Energy =  60.59   

 *** AUTO STEP TIME:  NEXT TIME INC = 0.10000E-04  UNCHANGED

     NONLINEAR DIAGNOSTIC DATA HAS BEEN WRITTEN TO  FILE: file.nd003

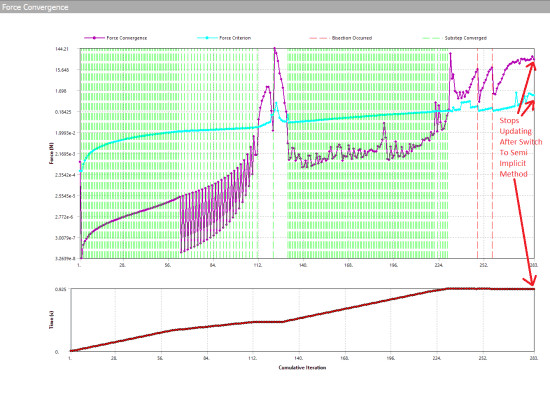
There are some ‘symptoms’ of the switch from implicit to explicit.  The most obvious is probably that the force convergence plot will stop updating. 

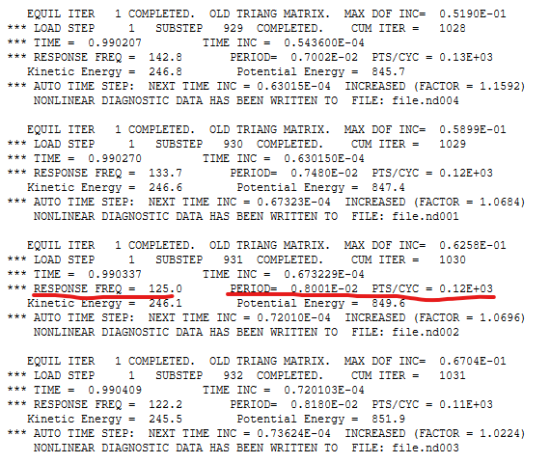
Changing the Solution Output to the Solver Output will show the explicit scheme being used in that case.  The telltale is the information on Response Frequency and Period (the example shown is a static structural solution).

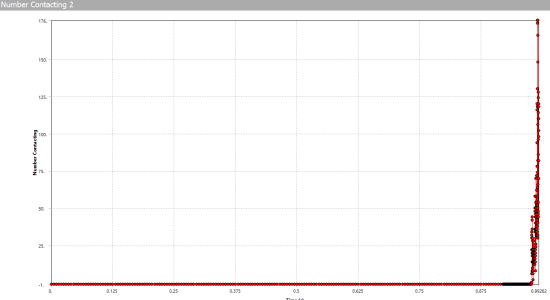
Deformation plot trackers and contact trackers continue to work as expected during the solution, however.

Using the semi-implicit method, the solution was able to successfully converge to the full load, and converged results are available at the last time point:

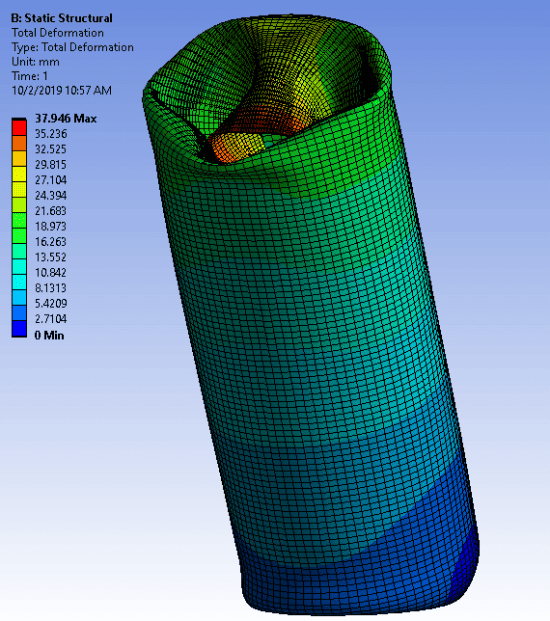
We also used the new keyframe animation technique to animate the results time history.

The semi-implicit method is well documented within the Mechanical APDL 2019 R2 Help, in the Advanced Analysis Guide, chapter 3 on Semi-Implicit Method.  We suggest reviewing that information to get a much better handle on the technique.

We hope this is helpful in getting your nonlinear solutions to converge the full value of applied loads.