In part 1 of this two-part post, I reviewed the challenges in the constitutive modeling of 3D printed parts using the Fused Deposition Modeling (FDM) process. In this second part, I discuss some of the approaches that may be used to enable analyses of FDM parts even in presence of these challenges. I present them below in increasing order of the detail captured by the model.
- Conservative Value: The simplest method is to represent the material with an isotropic material model using the most conservative value of the 3 directions specified in the material datasheet, such as the one from Stratasys shown below for ULTEM-9085 showing the lower of the two modulii selected. The conservative value can be selected based on the desired risk assessment (e.g. lower modulus if maximum deflection is the key concern). This simplification brings with it a few problems:
- The material property reported is only good for the specific build parameters, stacking and layer thickness used in the creation of the samples used to collect the data
- This gives no insight into build orientation or processing conditions that can be improved and as such has limited value to an anlayst seeking to use simulation to improve part design and performance
- Finally, in terms of failure prediction, the conservative value approach disregards inter-layer effects and defects described in the previous blog post and is not recommended to be used for this reason

- Orthotropic Properties: A significant improvement from an isotropic assumption is to develop a constitutive model with orthotropic properties, which has properties defined in all three directions. Solid mechanicians will recognize the equation below as the compliance matrix representation of the Hooke’s Law for an orthortropic material, with the strain matrix on the left equal to the compliance matrix by the stress matrix on the right. The large compliance matrix in the middle is composed of three elastic modulii (E), Poisson’s ratios (v) and shear modulii (G) that need to be determined experimentally.
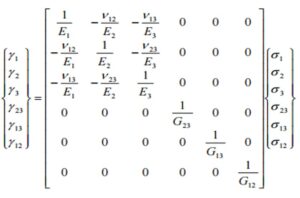
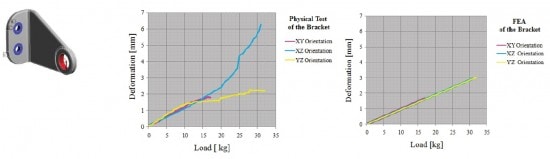
Good agreement between numerical and experimental results can be achieved using orthotropic properties when the structures being modeled are simple rectangular structures with uniaxial loading states. In addition to require extensive testing to collect this data set (as shown in this 2007 Master’s thesis), this approach does have a few limitations. Like the isotropic assumption, it is only valid for the specific set of build parameters that were used to manufacture the test samples from which the data was initially obtained. Additionally, since the model has no explicit sense of layers and inter-layer effects, it is unlikely to perform well at stresses leading up to failure, especially for complex loading conditions. This was shown in a 2010 paper that demonstrated these limitations in the analysis of a bracket that itself was built in three different orientations. The authors concluded however that there was good agreement at low loads and deflections for all build directions, and that the margin of error as load increased varied across the three build orientations.
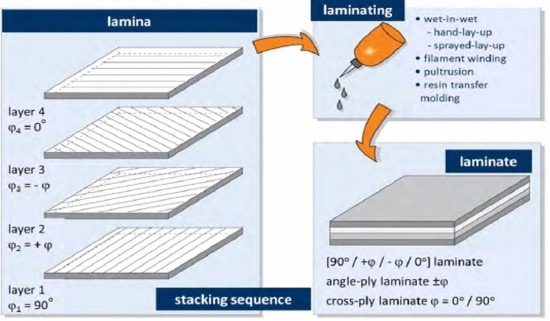
- Laminar Composite Theory: The FDM process results in structures that are very similar to laminar composites, with a stack of plies consisting of individual fibers/filaments laid down next to each other. The only difference is the absence of a matrix binder – in the FDM process, the filaments fuse with neighboring filaments to form a meso-structure. As shown in this 2014 project report, a laminar approach allows one to model different ply raster angles that are not possible with the orthotropic approach. This is exciting because it could expand insight into optimizing raster angles for optimum performance of a part, and in theory reduce the experimental datasets needed to develop models. At this time however, there is very limited data validating predicted values against experiments. ANSYS and other software that have been designed for composite modeling (see image below from ANSYS Composite PrepPost) can be used as starting points to explore this space.
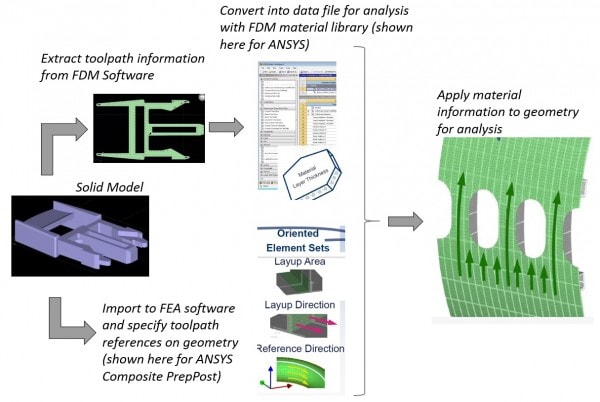
- Hybrid Tool-path Composite Representation: One of the limitations of the above approach is that it does not model any of the details within the layer. As we saw in part 1 of this post, each layer is composed of tool-paths that leave behind voids and curvature errors that could be significant in simulation, particularly in failure modeling. Perhaps the most promising approach to modeling FDM parts is to explicitly link tool-path information in the build software to the analysis software. Coupling this with existing composite simulation is another potential idea that would help reduce computational expense. This is an idea I have captured below in the schematic that shows one possible way this could be done, using ANSYS Composite PrepPost as an example platform.
Discussion: At the present moment, the orthotropic approach is perhaps the most appropriate method for modeling parts since it is allows some level of build orientation optimization, as well as for meaningful design comparisons and comparison to bulk properties one may expect from alternative technologies such as injection molding. However, as the application of FDM in end-use parts increases, the demands on simulation are also likely to increase, one of which will involve representing these materials more accurately than continuum solids.