Updated (8/30/2016): Two corrections made following suggestions by Gilbert Peters: the first corrects the use of honeycomb structures in radiator grille applications as being for flow conditioning, the second corrects the use of the Maxwell stability criterion, replacing the space frame example with an octet truss.
~
This is my first detailed post in a series on cellular structures for additive manufacturing, following an introductory post I wrote where I classified the research landscape in this area into four elements: design, analysis, manufacturing and implementation.
Within the design element, the first step in implementing cellular structures in Additive Manufacturing (AM) is selecting the appropriate unit cell(s). The unit cell is selected based on the performance desired of it as well as the manufacturability of the cells. In this post, I wish to delve deeper into the different types of cellular structures and why the classification is important. This will set the stage for defining criteria for why certain unit cell designs are preferable over others, which I will attempt in future posts. This post will also explain in greater detail what a “lattice” structure, a term that is often erroneously used to describe all cellular solids, truly is.
1. Honeycomb
1.1 Definition
Honeycombs are prismatic, 2-dimensional cellular designs extruded in the 3rd dimension, like the well-known hexagonal honeycomb shown in Figure 1. All cross-sections through the 3rd dimension are thus identical, making honeycombs somewhat easy to model. Though the hexagonal honeycomb is most well known, the term applies to all designs that have this prismatic property, including square and triangular honeycombs. Honeycombs have a strong anisotropy in the 3rd dimension – in fact, the modulus of regular hexagonal and triangular honeycombs is transversely isotropic – equal in all directions in the plane but very different out-of-plane.
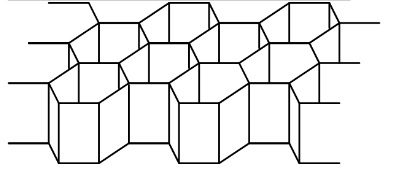

1.2 Design Implications
The 2D nature of honeycomb structures means that their use is beneficial when the environmental conditions are predictable and the honeycomb design can be oriented in such a way to extract maximum benefit. One such example is the crash structure in Figure 2 as well as a range of sandwich panels. Several automotive radiator grilles are also of a honeycomb design to condition the flow of air. In both cases, the direction of the environmental stimulus is known – in the former, the impact load, in the latter, airflow.
2. Open-Cell Foam
2.1 Definition
Freeing up the prismatic requirement on the honeycomb brings us to a fully 3-dimensional open-cell foam design as shown in one representation of a unit cell in Figure 3. Typically, open-cell foams are bending-dominated, distinguishing them from stretch-dominated lattices, which are discussed in more detail in a following section on lattices.
2.2 Design Implications
Unlike the honeycomb, open cell foam designs are more useful when the environmental stimulus (stress, flow, heat) is not as predictable and unidirectional. The bending dominated mechanism of deformation make open-cell foams ideal for energy absorption – stretch dominated structures tend to be stiffer. As a result of this, applications that require energy absorption such as mattresses and crumple zones in complex structures. The interconnectivity of open-cell foams also makes them a candidate for applications requiring fluid flow through the structure.


3. Closed-Cell Foam
As the name suggests, closed cell foams are open-cell foams with enclosed cells, such as the representation shown in Figure 6. This typically involves a membrane like structure that may be of varying thickness from the strut-like structures, though this is not necessary. Closed-cell foams arise from a lot of natural processes and are commonly found in nature. In man-made entities, they are commonly found in the food industry (bread, chocolate) and in engineering applications where the enclosed cell is filled with some fluid (like air in bubble wrap, foam for bicycle helmets and fragile packaging).
3.2 Design Implications
The primary benefit of closed cell foams is the ability to encapsulate a fluid of different properties for compressive resilience. From a structural standpoint, while the membrane is a load-bearing part of the structure under certain loads, the additional material and manufacturing burden can be hard to justify. Within the AM context, this is a key area of interest for those exploring 3D printing food products in particular but may also have value for biomimetic applications.

4. Lattice
4.1 Definition
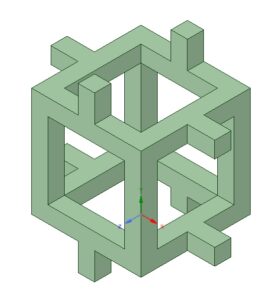
Lattices are in appearance very similar to open cell foams but differ in that lattice member deformation is stretch-dominated, as opposed to bending*. This is important since for the same material allocation, structures tend to be stiffer in tension and/or compression compared to bending – by contrast, bending dominated structures typically absorb more energy and are more compliant.
So the question is – when does an open cell foam become stretch dominated and therefore, a lattice? Fortunately, there is an app equation for that.
Maxwell’s Stability Criterion
Maxwell’s stability criterion involves the computation of a metric M for a lattice-like structure with b struts and j joints as follows:
In 2D structures: M = b – 2j + 3
In 3D structures: M = b – 3j + 6
Per Maxwell’s criterion, for our purposes here where the joints are locked (and not pinned), if M < 0, we get a structure that is bending dominated. If M >= 0, the structure is stretch dominated. The former constitutes an open-cell foam, the latter a lattice.
There are several approaches to establishing the appropriateness of a lattice design for a structural applications (connectivity, static and kinematic determinism etc.) and how they are applied to periodic structures and space frames. It is easy for one (including for this author) to confuse these ideas and their applicability. For the purposes of AM, Maxwell’s Stability Criterion for 3D structures is a sufficient condition for static determinancy. Further, for a periodic structure to be truly space-filling (as we need for AM applications), there is no simple rigid polyhedron that fits the bill – we need a combination of polyhedra (such as an octahedron and tetrahedron in the octet truss shown in the video below) to generate true space filling, and rigid structures. The 2001 papers by Deshpande, Ashby and Fleck illustrate these ideas in greater detail and are referenced at the end of this post.
Video: The octet truss is a classic stretch-dominated structure, with b = 36 struts, j = 14 joints and M = 0 [Attr. Lawrence Livermore National Labs]
4.2 Design Implications
Lattices are the most common cellular solid studied in AM – this is primarily on account of their strong structural performance in applications where high stiffness-to-weight ratio is desired (such as aerospace), or where stiffness modulation is important (such as in medical implants). However, it is important to realize that there are other cellular representations that have a range of other benefits that lattice designs cannot provide.
Conclusion: Why this matters
It is a fair question to ask why this matters – is this all just semantics? I would like to argue that the above classification is vital since it represents the first stage of selecting a unit cell for a particular function. Generally speaking, the following guidelines apply:
- Honeycomb structures for predictable, unidirectional loading or flow
- Open cell foams where energy absorption and compliance is important
- Closed cell foams for fluid-filled and hydrostatic applications
- Lattice structures where stiffness and resistance to bending is critical
Finally, another reason it is important to retain the bigger picture on all cellular solids is it ensures that the discussion of what we can do with AM and cellular solids includes all the possibilities and is not limited to only stiffness driven lattice designs.
Note: This blog post is part of a series on “Additive Manufacturing of Cellular Solids” that I am writing over the coming year, diving deep into the fundamentals of this exciting and fast evolving topic. To ensure you get each post (~2 a month) or to give me feedback for improvement, please connect with me on LinkedIn.
References
[1] Ashby, “Materials Selection in Mechanical Design,” Fourth Edition, 2011
[2] Gibson & Ashby, “Cellular Solids: Structure & Properties,” Second Edition, 1997
[3] Gibson, Ashby & Harley, “Cellular Materials in Nature & Medicine,” First Edition, 2010
[4] Ashby, Evans, Fleck, Gibson, Hutchinson, Wadley, “Metal Foams: A Design Guide,” First Edition, 2000
[5] Deshpande, Ashby, Fleck, “Foam Topology Bending versus Stretching Dominated Architectures,” Acta Materialia 49, 2001
[6] Deshpande, Fleck, Ashby, “Effective properties of the octet-truss lattice material,” Journal of the Mechanics and Physics of Solids, 49, 2001
Notes
* We defer to reference [1] in distinguishing lattice structures as separate from foams – this is NOT the approach used in [2] and [3] where lattices are treated implicitly as a subset of open-cell foams. The distinction is useful from a structural perspective and as such is retained here.