Do those pesky mid-side nodes really do anything other than increase my node count and runtime? Over the years, I have heard that question over and over. “Do I really need them?” If you are using tetra elements, then the answer is absolutely, “Yes!” They even do more than just give you nice curvature to follow your geometry. For tetras, the midside nodes are necessary to predict proper stresses. Lower ordered tetras are overly stiff and will under predict deflection and stresses. Let’s look at the underlying equations that make up the shape functions in both element types.
Yeah, the equations for tetras are a little more complicated than that, but I really didn’t think you wanted to go down that road. But I will remind you that low-order elements have linear shape functions, while high-order elements have quadratic shape functions. So let’s look at an example, instead, to show that lower-order tetras will give unconservative results.
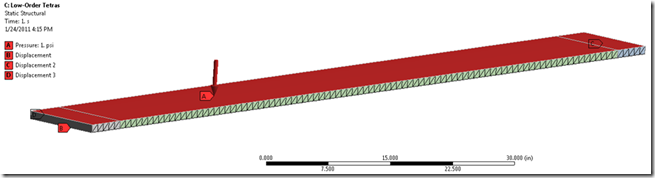
For the example, I made a simply-supported, rectangular-cross-section plank. It’s 100 inches long, by 10 inches wide, by 1 inch thick, with a 1 psi pressure load. I set the mesh size at 1 inch and solved with low-order tetras, high-order tetras, and also with low and high-order hex elements. The results are tabulated below along with the hand-calculated solution from the 7th Edition of Roark’s Formulas for Stress and Strain, Table 8.1, case 2e.
| Deflection | Def. % Diff | Stress | Stress % Diff | Nodes | Elements | |
| Roark’s | -0.53864 | 7500.0 psi | ||||
| 20-Node Hex | -0.54159 | 0.55% | 7527.0 psi | 0.36% | 7553 | 1,000 |
| 8-Node Hex | -0.54142 | 0.52% | 7529.5 psi | 0.39% | 2222 | 1,000 |
| 10-Node Tetra | -0.54158 | 0.55% | 7525.9 psi | 0.35% | 20661 | 11,998 |
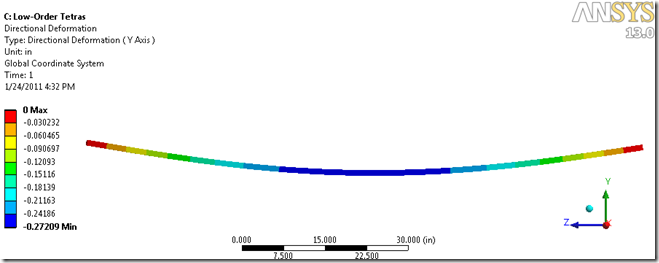
| 4-Node Tetra* | -0.27151 | –49.6% | 2249.3 psi | –70.0% | 3222 | 11,999 |
As you can see, the hex elements along with the 10-node tetras get close to the solution and provide conservative results. The 4-node tetras, however, which are actually degenerate 8-node hex elements because ANSYS removed their 4-node tetra elements along time ago, show only half the deflection under the same load. The extra stiffness also causes the modal frequencies to be higher. In this case, the frequencies of the low-order tetras were about 40% higher than the high-order tetras. When you’re looking at operating ranges, this could also lead to unconservative conclusions.
Of course this is a pretty coarse mesh with only one element through the thickness. So how do the results change as the mesh is refined? We should only need to cut the element size by half to get the extra nodes and the same results, right?
| Deflection | Def. % Diff | Stress | Stress % Diff | Nodes | Elements | |
| Roark’s | -0.53864” | 7500.0 psi | ||||
| 1” | -0.27151” |
–49.6% |
2249.3 psi |
-70.0% |
3,222 | 11,999 |
| 0.5” | -0.39768” |
-26.2% |
4879.1 psi |
-34.9% |
17,624 | 77,612 |
| 0.3” | -0.47582” |
-11.7% |
6069.5 psi |
-19.1% |
69,040 | 334,433 |
| 0.2” | -0.51023” |
-5.3% |
6760.9 psi |
-9.8% |
213,122 | 1,105,641 |
| 0.1” | -0.53345” |
-0.96% |
7309.6 psi |
-2.5% |
1,599,327 | 8,877,326 |
As you can see the answer is, “No.” Because the high-order elements have quadratic shape functions , it takes far more linear elements to make up the difference. Here is a little animation to show why. You can see the error left by each set of linear elements when try to match a quadratic function.
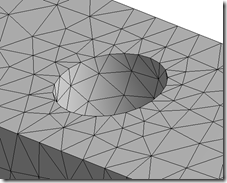
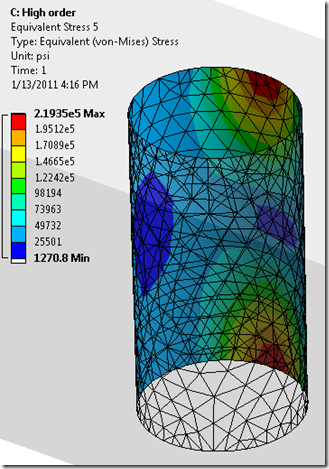
For another example, I made a long square-cross-section bar with holes in it. It is cantilevered with a shear load at the other end. I set the Physics preference to Mechanical and the Relevance Center to ‘Fine’ and I got the mesh that you see below. (I’d say its not too bad for 15 seconds of works. )
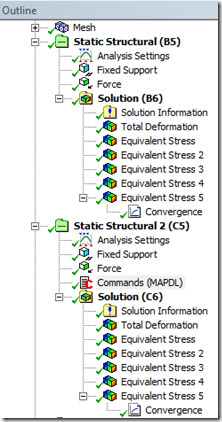
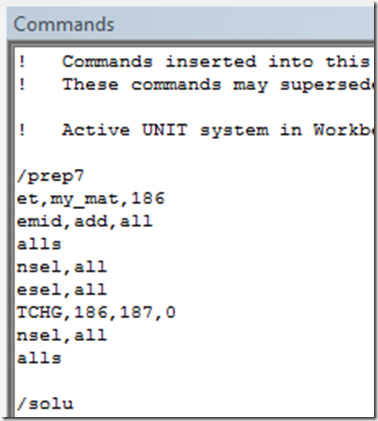
Just to make sure that my mesh was the same in both cases, I told Mechanical to Drop the midside nodes and then I added a Command Object in the high-order case to convert the elements to Solid 187 tetras during the run. Since no geometry is sent from Mechanical, the midside nodes were added and the edges were kept straight, so no further curvature was picked up. Here’s the command object to try out yourself.
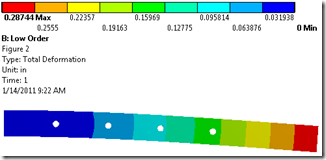
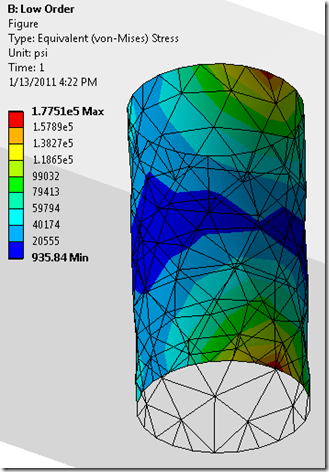
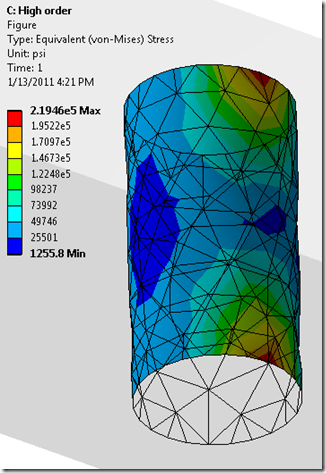
By scoping the results to just the hole closest to the fixed end we can see the difference in the stress values for the two runs. The low-order tetras yield results that are 12% lower for deflection and over 19% lower for stress than the same mesh with midside nodes. (But look, Boss! I saved 4 seconds on the solve time!!!)
| Elements | Nodes | Total Deflection |
SEQV | Solver Runtime | |
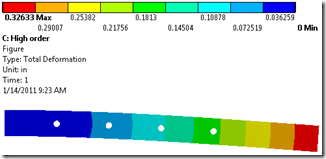
| Low-order | 18383 | 4854 | 0.28744” | 177.51 Ksi | 6.677 Sec. |
| High-order | 18383 | 31332 | 0.32633” | 219.46 Ksi | 10.951 Sec. |
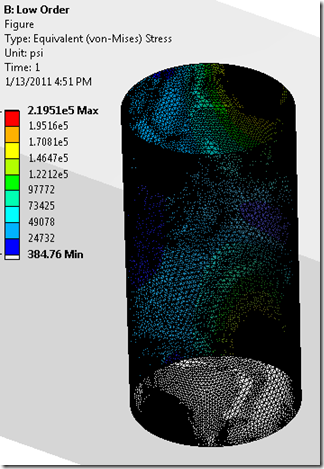
So how many low-order tetras are needed to get the same accuracy this time? I used the Convergence Tool in Workbench to find out this time. The Convergence tool refines the mesh only for the scoped region of the results plot. So the resultant mesh looks like this.
| Elements | Nodes | SEQV | Solver Runtime | |
| Low-order |
1,271,619 |
234,484 |
21.951 Ksi |
349.785 Sec. |
|
High-order |
18,383 |
31,332 |
21.946 Ksi |
10.951 Sec. |
The last pass took just under 6 minutes to run (349.8 sec). The stress finally gets as high as it is with the high-order elements, but the deflection results are still incorrect because the model was only refined at the hole. And say it with me, “If the deflection is wrong, then the stress ain’t gonna be right!!!” So basically I’ve wasted a half an hour getting the wrong solution so that you won’t have to do the same. Just remember, mid-side nodes are your friends. And just like any good friend, take advantage of them when you can!




![clip_image001[6] clip_image001[6]](/wp-content/uploads/oldblog/clip_image0016_thumb.jpg)