Part of my job at PADT is writing custom software for our various clients. We focus primarily on developing technical software for the engineering community, with a particular emphasis on tools that integrate with the ANSYS suite of simulation tools. Frankly, writing software is my favorite thing to do at PADT, simply because software development is all about problem solving.
This morning I got to work on a fairly simple feature of a much larger tool that I am currently developing. The feature I’m working on involves graphically editing polygons. Why, you ask am I doing this? Well, that I can’t say, but nonetheless I can share a particularly interesting problem (to me at least) that I got to take a swing at solving. The problem is this:
When a user is editing a node in the polygon by dragging it around on the screen, how do you handle the case when they drop it on an existing node?
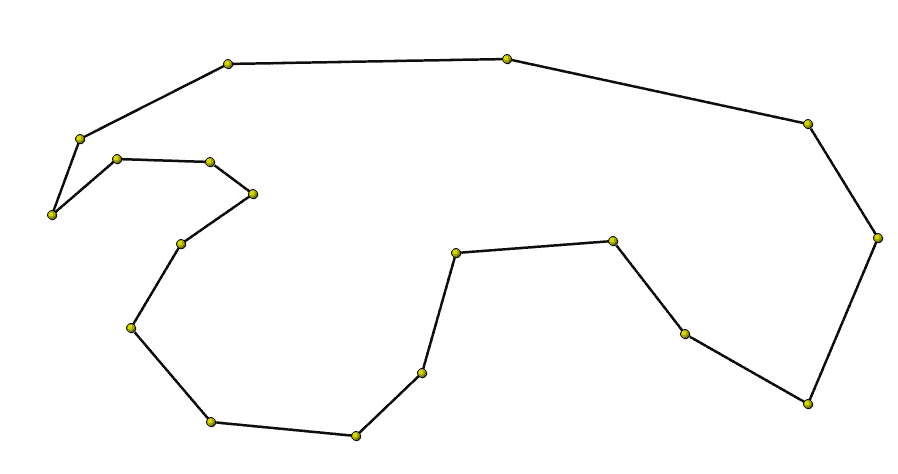
Consider this polygon I sketched out in a prototype of the tool.
What should happen if the user drags this node over on top of that node: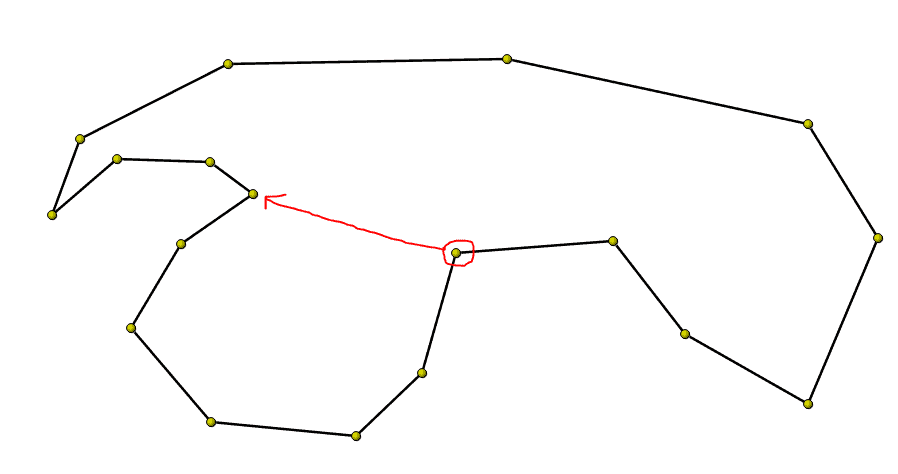
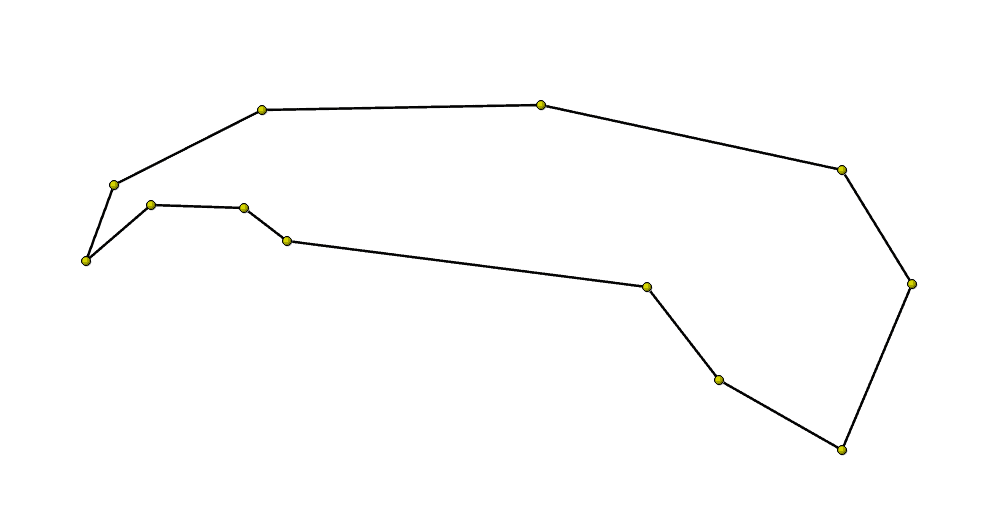
Well, I think the most logical thing to do is that you merge the two nodes together. Implementing that is pretty easy. The slightly harder question is what to do with the remaining structure of the polygon? For my use case, polygons have to be manifold in that no vertex is connected to more than two edges. (The polygons can be open and thus have two end vertices connected to only one edge.) So, what part do you delete? Well, my solution is that you delete the “smaller” part, where “smaller” is defined as the part that has the fewest nodes. So, for example, this is what my polygon looks like after the “drop”
Conceptually, this sounds pretty simple, but how do you do it programmatically? To give some background, note that the nodes in my polygon class are stored in a simple, ordered C++ std::list<>.
Now, I use a std::list<> simply because I know I’m going to be inserting and deleting nodes at random places. Linked lists are great for that, and for rendering, I have to walk the whole list anyway, so there’s no performance hit there. Graphically, my data structure looks
something like this:
Pretty simple. For a closed polygon, my class maintains a flag and simply draws an edge from the last node to the first node.
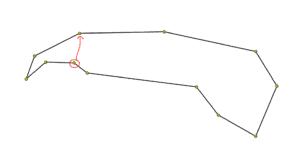
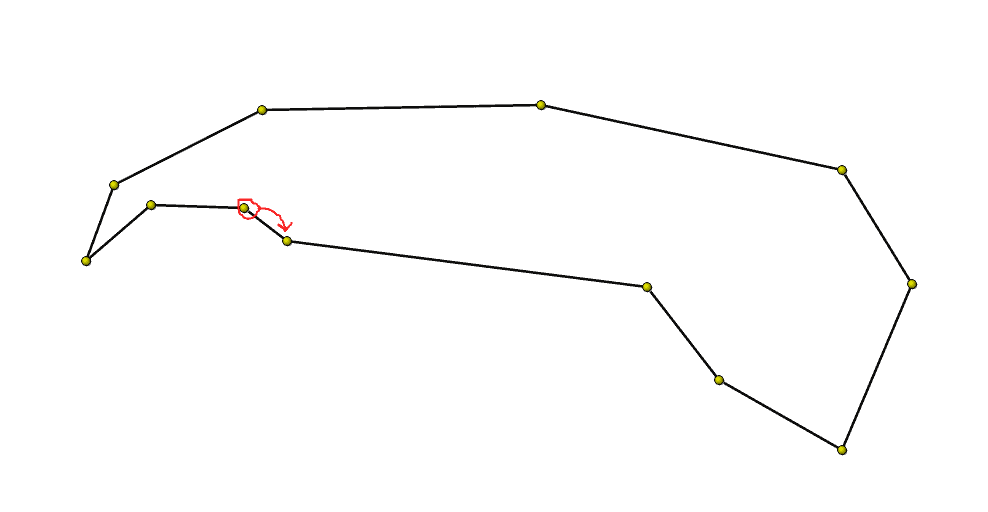
The rub comes when you start to realize that there are tons of different ways a user might try to merge nodes together in either an open or closed polygon. I’ve illustrated a few below along with what nodes would need to be merged in the corresponding data structure. In the data structure pictures, the red node is the target (the node on which the user will be dropping) and the green node is the one they are manipulating (the source node).
Here is one example:
Here is another example:
Finally, here is one more:
In all these examples, we have different “cases” that we need to handle. For instance, in the first example the portion of the data structure we want to keep is the stuff between the source and target nodes. So, the stuff on the “ends” of the list needs to be deleted. In the middle case, we just need to merge the source and target together. Finally, in the last case, the nodes between the source and target need to be deleted, whereas the stuff at the “ends” of the list need to be kept.
This simple type of problem causes shivers in many programmers, and I’ll admit, I was nervous at first that this problem was going to lead to a solution that handled each individual case respectively. Nothing in all of programming is more hideous than that. So, there has to be a simple way to figure out what part of the list to keep, and what part of the list to throw away.
Now, I’m sure this problem has been solved numerous times before, but I wanted to take a shot at it without googling. (I still haven’t googled, yet… so if this is similar to any other approach, they get the credit and I just reinvented the wheel…) I remember a long time ago listening to a C++ programmer espouse the wonders of the standard library’s algorithm section. I vaguely remember him droning on about how wonderful the std::rotate algorithm is. At the time, I didn’t see what all the fuss was about. Now, I’m right there with him. std::rotate is pretty awesome!
std::rotate is a simple algorithm. Essentially what it does is it takes the first element in a list, pops it off the list and moves it to the rear of the list. Everything else in the list shifts up one spot. This is called a left rotate, because you can imagine the items in the list rotating to the left until they get to the front of the line, at which point they fall off and are put back on the end of the list. (Using reverse iterators you can effectively perform a right rotate as well.) So, how can we take advantage of this to simplify figuring out what needs to be deleted from our list of nodes?
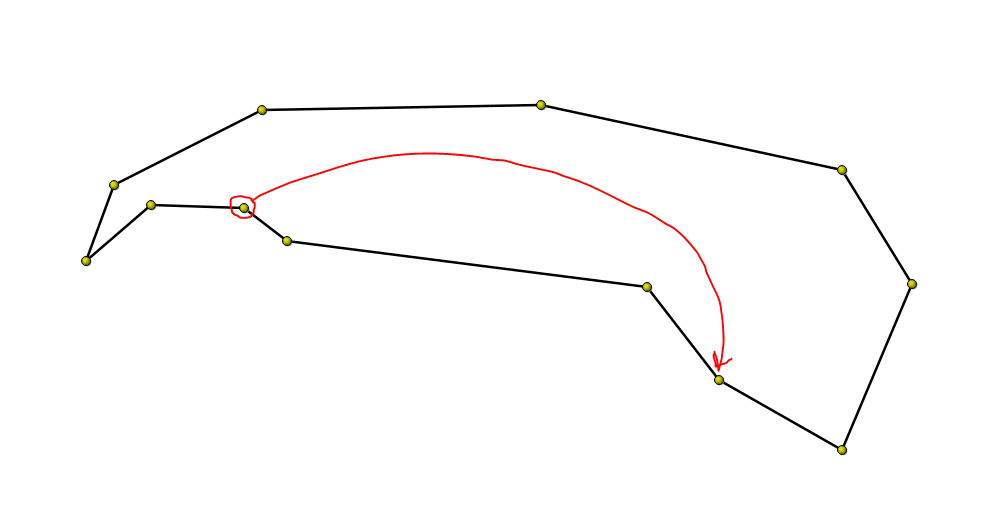
Well, the answer is remarkably simple. Once we locate the source and target nodes in the list, regardless of their relative position with respect to one another or to the ends of the list, we simply left rotate the list until the target becomes the head of the list. That is, if we start with this:
We left rotate until we have this:
That’s great, but what does that buy us? Well, now that one of the participating nodes is at the head of the list, our problem is much simpler because all of the nodes that we need to delete are now at either end of the list. The only question left to answer is which end of the list do we trim off? The answer to that question is trivial. We simply trim off the shorter end of the list with respect to the source node (the green node in the diagram). The “lengths” of the two lists are defined as follows. For the head section, it’s the number of nodes up to, but not including the source. (This section obviously includes the target node) For the tail, it’s the number of nodes from the source to the end, including the source. (This section includes the source node). Since we define the two sections this way we are guaranteed to delete either the source or the target, but not both. Its fine to delete either one of them, because at this point we’ve deemed the geometrically coincident, but we must not accidentally delete both!!
In the example just given, after the rotate, we would delete the head of the list. However, let’s take a look at our first example. Here is the original list:
Here is the rotated list:
So, in this case, the “end” of the list (including the source) is the shortest. If it is a tie, then it doesn’t matter, just pick one. Interestingly enough, if the two nodes are adjacent in the original list, then the rotated list will look like either this:
Or this, if the source is “before” the target in the original list:
In either case, the algorithm works unchanged, and we only delete one node. It’s beautiful! (At least in my opinion…) Modern C++ makes this type of code really clean and easy to write. Here is the entire thing, including the search to located geometrically adjacent nodes as well as the merge. The standard library algorithms really help out!
// Search lambda function for looking for any other node in the list that is
// coindicent to this node, except this node.
auto searchAdjacentFun = [this, pNode](const NodeListTool::AdjustNodePtrT &pOtherNode)->bool
{
if (pNode->tag() == pOtherNode->tag()) return false;
return (QVector2D(pNode->pos() - pOtherNode->pos()).length() < m_snapTolerance); }; auto targetLoc = std::find_if(m_nodes.begin(), m_nodes.end(), searchAdjacentFun); // If we don't find an adjacent node within the tolerance, then we can't merge if (targetLoc == m_nodes.end()) { return false; } // Tidy things up so that the source has exactly the same position as the target pNode->setPos((*targetLoc)->pos());
// Begin the merge by left rotating the target so that it is at the
// beginning of the list
std::rotate(m_nodes.begin(), targetLoc, m_nodes.end());
// Find this node in the list
auto searchThis = [this, pNode](const NodeListTool::AdjustNodePtrT &pOtherNode)->bool
{
return (pNode->tag() == pOtherNode->tag());
};
auto sourceLoc = std::find_if(m_nodes.begin(), m_nodes.end(), searchThis);
// Now, figure out which nodes we are going to delete.
auto distToBeg = std::distance(m_nodes.begin(), sourceLoc);
auto distToEnd = std::distance(sourceLoc, m_nodes.end());
if (distToBeg < distToEnd) { // If our source is closer to the beginning (which is the target) // than it is to the end of the list, then we need to delete // the nodes at the front of the list m_nodes.erase(m_nodes.begin(), sourceLoc); } else { // Otherwise, delete the nodes at the end of the list m_nodes.erase(sourceLoc, m_nodes.end()); } // Now, see if we still have more than 2 vertices if (m_nodes.size() > 2) {
m_bClosed = true;
}
else {
m_bClosed = false;
}
return true;
